广义相对论的基本框架张朝阳博士首先回顾了广义相对论的基本框架，广义相对论表明，物质的存在会导致时空弯曲，在弯曲时空中的粒子运动时，不需要考虑引力作用，而是需要在时空弯曲中运动，利用称为度规的二阶张量，可以描述时空弯曲，度规的一阶导数定义了克氏符，用于描述基矢随坐标的变化，再次对克氏符求导并按特定方式组合，可以定义空间的黎曼曲率，由此确...。

广义相对论的基本框架广义相对论表明物质的存在导致时空弯曲，粒子在弯曲时空中的运动不是受到引力这样的外力，而是沿着时空中最短的路径运动，可以使用一个二阶张量，即度规，来描述时空中弯曲，度规的一阶导数可以定义克氏符，进而可以描述基矢随坐标的变化，再对克氏符求一次导数并以特定方式进行组合，可以定义空间的黎曼曲率，时空是否弯曲正由黎曼曲率来决...。

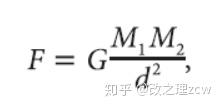
广义相对论的基本框架广义相对论表明物质的存在导致时空弯曲，时空的弯曲可以用一个二阶张量即度规来描述，度规的一阶导数可以定义克氏符，进而可以描述基矢随坐标的变化，再对克氏符求一次导数并以特定方式进行组合，可以定义空间的黎曼曲率，时空是否弯曲正由黎曼曲率来决定，黎曼曲率实际上由度规的二阶导数组成，如果黎曼曲率为0，说明时空是，局域，平直的...。

引力波的作用时空扭曲相对论的基本框架广义相对论表明物质的存在导致时空弯曲，时空的弯曲可以用一个二阶张量，度规，描述，度规的一阶导数定义克氏符，克氏符的二阶导数定义黎曼曲率，黎曼曲率为0表示时空是平直的，黎曼曲率不为0表示时空是弯曲的，爱因斯坦场方程描述物质存在与时空弯曲的关系，时空弯曲如果已知度规，可以通过计算克氏符和黎曼曲率来得到时...。

作者，张朝阳广义相对论的基本框架广义相对论表明物质的存在导致时空弯曲，当探究粒子在弯曲时空中的运动时，可以放下其受到引力这样的观点，而直接地认为粒子需要在这弯曲的时空中走出一条最短的线，借助一个二阶张量即度规可以描述时空的弯曲，度规的一阶导数可以定义克氏符，进而可以描述基矢随坐标的变化，再对克氏符求一次导数并以特定方式进行组合，可以定...。

张朝阳求解弱场引力波方程引力波的本质和作用引力波是一种时空中涟漪状的扰动，由大质量物体加速运动产生，它们以光速在宇宙中传播，对其他物体产生引力效应，引力波的具体形式广义相对论表明，物质存在会导致时空弯曲，度规是描述时空弯曲的一种数学工具，其二阶导数组成黎曼曲率，当时空是微弱弯曲时，度规的微扰满足以下波动方程，html∇^2h，μν，∂...。

张朝阳教授的引力波课程广义相对论的基本框架广义相对论认为物质导致时空弯曲，时空弯曲可以描述为度规的微扰，度规的微扰满足波动方程，其解可以求得度规的具体形式，度规的一阶导数定义为克氏符，克氏符的二阶导数定义为黎曼曲率，黎曼曲率决定了时空是否弯曲，爱因斯坦场方程描述了度规与物质存在之间的关系，引力波的具体形式爱因斯坦预言引力波的存在，引力...。

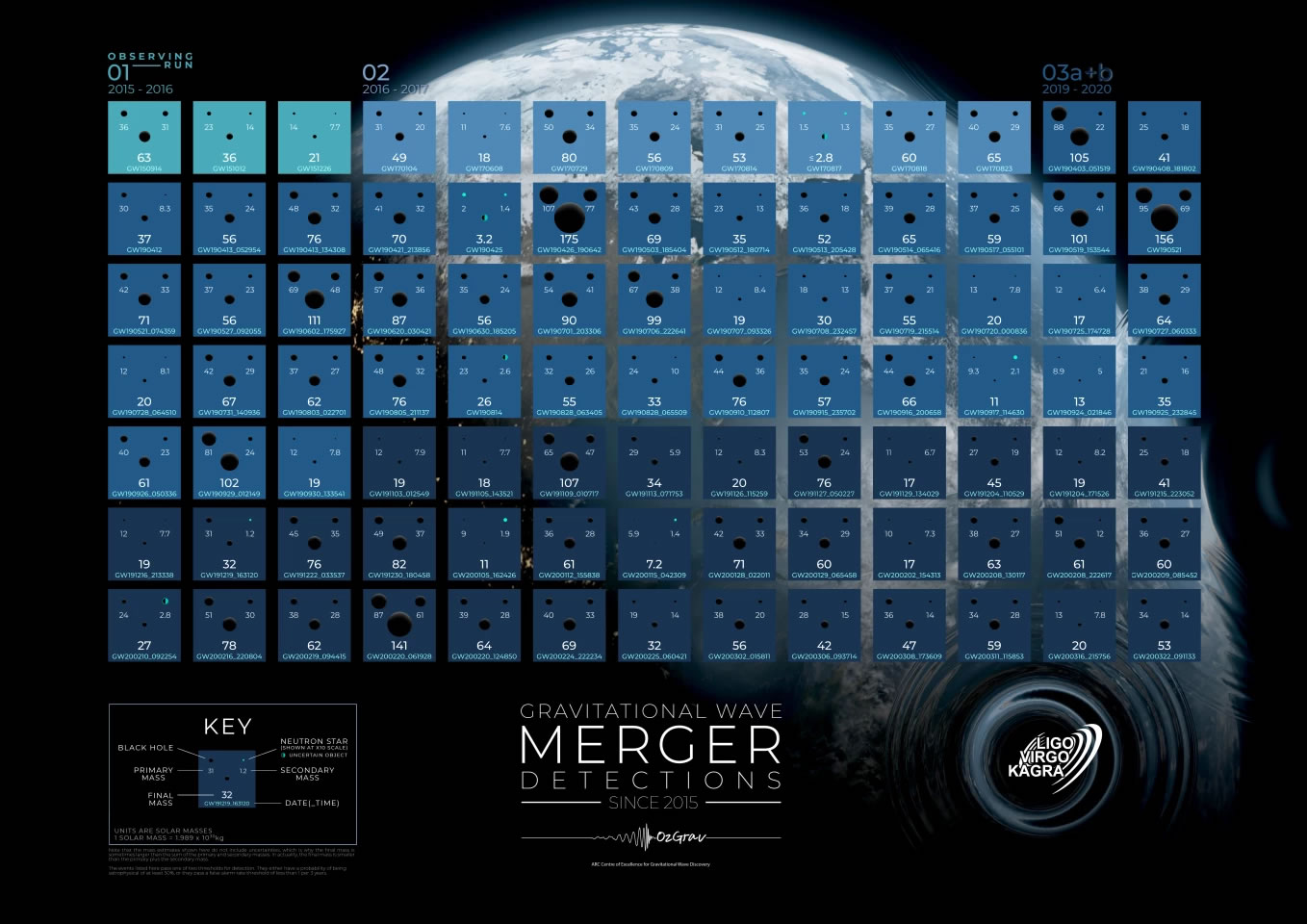
广义相对论的基本框架广义相对论表明，物质的存在导致时空弯曲，当探究粒子在弯曲时空中的运动时，可以放下其受到引力这样的观点，而直接地认为粒子需要在这弯曲的时空中走出一条最短的线，借助一个二阶张量即度规可以描述时空的弯曲，度规的一阶导数可以定义克氏符，进而可以描述基矢随坐标的变化，再对克氏符求一次导数并以特定方式进行组合，可以定义空间的黎...。

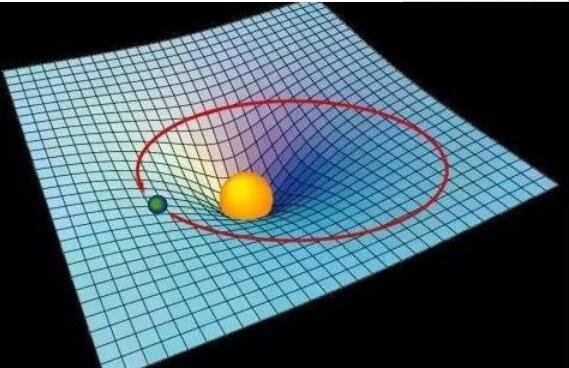
广义相对论的基本框架广义相对论认为物质的存在导致时空弯曲，粒子在弯曲时空中的运动不是受到引力，而是走出一条最短的线，可以通过度规描述时空的弯曲，一阶导数定义克氏符，再求导得到黎曼曲率，由黎曼曲率决定时空是否弯曲，度规具体形式由爱因斯坦场方程给出，里奇张量是场方程的一部分，引力波的具体形式爱因斯坦预言引力波的存在，它是一种时空弯曲的波动...。

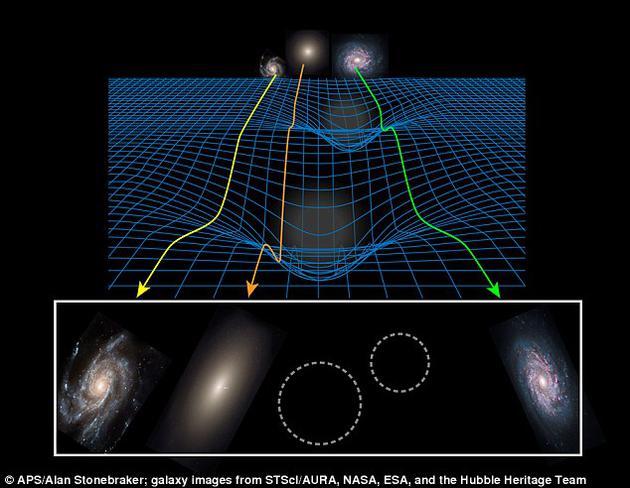
引力波的概念引力波是一种时空涟漪，由物体加速运动引起，它与电磁波相似，但与电磁波不同，引力波与物质的相互作用极弱，具有极强的穿透力，广义相对论基本框架广义相对论认为，物质的存在导致时空弯曲，时空弯曲描述了物体运动的最短路径，为了描述时空弯曲，需要一个二阶张量称为度规，度规的一阶导数可以定义克氏符，描述基矢随坐标的变化，克氏符的二阶导数...。

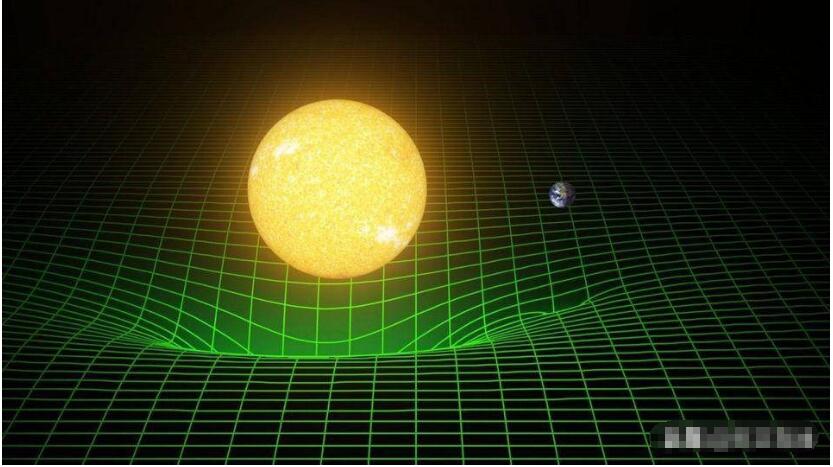
广义相对论的基本框架广义相对论表明，物质的存在会引起时空弯曲，在弯曲时空中的粒子运动不受引力作用，而是沿着最短路径移动，时空的弯曲可以用度规张量描述，度规的一阶导数为克里斯托费尔符号，它描述了基矢随坐标的变化，克里斯托费尔符号的二阶导数可以定义黎曼曲率，它决定了时空是否弯曲，黎曼曲率由度规的二阶导数组成，如果黎曼曲率为0，表明时空是平...。

广义相对论的基本框架张朝阳首先带领大家回顾了广义相对论的基本框架，广义相对论表明物质的存在导致时空弯曲，当探究粒子在弯曲时空中的运动时，可以放下其受到引力这样的观点，而直接地认为粒子需要在这弯曲的时空中走出一条最短的线，借助一个二阶张量即度规可以描述时空的弯曲，度规的一阶导数可以定义克氏符，进而可以描述基矢随坐标的变化，再对克氏符求一...。

广义相对论的基本框架广义相对论表明，物质的存在导致时空弯曲，当探究粒子在弯曲时空中的运动时，可以放下其受到引力这样的观点，而直接地认为粒子需要在这弯曲的时空中走出一条最短的线，借助一个二阶张量即度规可以描述时空的弯曲，度规的一阶导数可以定义克氏符，进而可以描述基矢随坐标的变化，再对克氏符求一次导数并以特定方式进行组合，可以定义空间的黎...。

广义相对论的基本框架广义相对论表明物质的存在导致时空弯曲，当探究粒子在弯曲时空中的运动时，可以放下其受到引力这样的观点，而直接地认为粒子需要在这弯曲的时空中走出一条最短的线，借助一个二阶张量即度规可以描述时空的弯曲，度规的一阶导数可以定义克氏符，进而可以描述基矢随坐标的变化，再对克氏符求一次导数并以特定方式进行组合，可以定义空间的黎曼...。

张朝阳推导引力波的具体形式广义相对论的基本框架广义相对论表明，物质的存在会导致时空弯曲，要描述时空的弯曲程度，物理学家使用一个称为度规的二阶张量，度规的导数可以定义克氏符，克氏符的变化又可以定义黎曼曲率，黎曼曲率决定了时空是否弯曲，爱因斯坦场方程描述了度规与物质存在之间的关系，通过求解爱因斯坦场方程，可以得到时空弯曲的具体形式，度规的...。

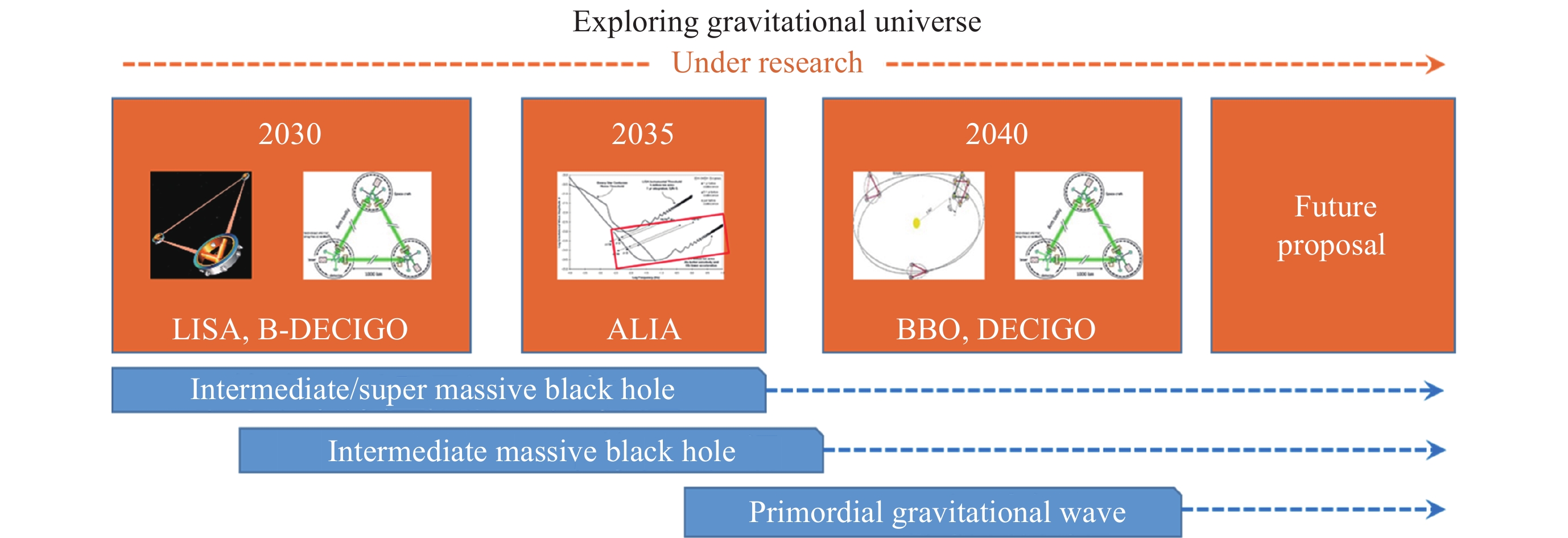
广义相对论基本框架回顾广义相对论表明，物质的存在会导致时空弯曲，粒子的运动不再遵循引力作用下的轨迹，而是沿着弯曲时空中的最短路径运动，时空的弯曲可以用度规这个二阶张量来描述，度规的一阶导数定义了克氏符，描述了基矢随坐标的变化，克氏符的二次导数定义了黎曼曲率，表示时空是否弯曲，黎曼曲率由度规的二阶导数组成，如果黎曼曲率为零，时空是平直的...。

广义相对论的基本框架广义相对论表明，物质的存在导致时空弯曲，时空弯曲可以通过度规来描述，度规的一阶导数定义克氏符，克氏符的二阶导数定义黎曼曲率，黎曼曲率描述时空的弯曲程度，由度规的二阶导数组成，爱因斯坦场方程爱因斯坦场方程描述了度规与物质存在之间的关系，里奇张量是黎曼曲率的缩并，观测效应，引力波导致测试粒子在时空中的轨迹偏离，可以通过...。

张朝阳，搜狐创始人、董事局主席兼首席执行官、物理学博士，在，张朝阳的物理课，第二百三十二期中，具体求解了度规的形式，介绍了引力波的两种模式，并利用测地偏离方程介绍了引力波导致的可观测效应，广义相对论的基本框架广义相对论表明物质的存在导致时空弯曲，时空弯曲可以用度规来描述，度规的一阶导数可以定义克氏符，进而可以描述基矢随坐标的变化，再对...。

理解纳维尔，斯托克斯方程前言纳维尔，斯托克斯方程是描述流体的运动和行为的基本方程之一，它是一个偏微分方程组，用于计算流体的速度、压力和温度等物理量，纳维尔，斯托克斯方程纳维尔，斯托克斯方程可以写成以下形式，ρ，∂u，∂t，u·∇u，=，∇p，μ∇²u，λ，μ，∇，∇·u，其中，ρ是流体的密度u是流体的速度矢量t是时间p是流体的压力μ...。

引言纳维尔，斯托克斯方程是流体力学中的基本方程之一，它描述了流体的运动状态，对于非专业人士来说，理解纳维尔，斯托克斯方程可能会有一些困难，本文将从基础出发，一步步解析纳维尔，斯托克斯方程，并利用张量语言对其进行简化，让读者能够更深入地理解流体力学中的基本原理，矢量微积分与微分几何在学习纳维尔，斯托克斯方程之前，我们需要先了解矢量微积分...。

纳维尔，斯托克斯方程是描述流体运动的核心方程，但它的表述形式复杂，难以理解，通过张量语言的简化，我们可以更透彻地理解其内涵，与牛顿运动定律的联系纳维尔，斯托克斯方程实质上是牛顿第三定律在流体中的表达，牛顿第三定律指出，作用力与反作用力在大小上相等、方向相反，在流体中，作用力表现在两种形式，压力梯度项和粘滞项，压力梯度项描述流体内部压力...。

AI竞赛升温，英伟达、马斯克和扎克伯格争夺GPU英伟达持续主导数据中心GPU市场根据英伟达的数据，2023年公司与AI工作负载相关的英伟达数据中心部门的销售收入为184亿美元，同比增长409%，英伟达在数据中心GPU市场的份额约为98%，主要归功于其旗舰H100芯片几乎没有竞争对手，Blackwell受到热捧，全球GPU市场前景光明2...。

理解纳维尔，斯托克斯方程纳维尔，斯托克斯方程是一组微分方程，描述了流体的运动，它们由克劳德，路易·纳维尔和乔治·加布里埃尔·斯托克斯于19世纪初独立提出，方程描述纳维尔，斯托克斯方程描述了流体中任一点的速度、压力和应力的关系，它们由以下公式表示，ρ，∂u，∂t，u·∇u，=，∇p，μ∇2u，ρg其中，ρ是流体的密度u是流体的速度p是流...。

理解纳维尔，斯托克斯方程，张量语言的简化1.纳维尔，斯托克斯方程的本质纳维尔，斯托克斯方程是流体力学中的基本方程，描述了流体运动的方程，它是一个矢量微分方程，涉及流体的速度、压力、粘度和密度，方程的形式为，ρ，∂v，∂t，=，∇p，μ∇^2v，ρg其中，ρ是流体的密度v是流体的速度p是流体的压力μ是流体的粘度g是重力加速度2.与牛顿运...。

纳维尔，斯托克斯方程在流体力学中具有重要意义，它描述了流体的运动行为，理解该方程并非易事，本篇文章将利用张量语言，帮助读者简化流体力学中的矢量计算，并深入理解纳维尔，斯托克斯方程与牛顿运动定律之间的关联，矢量微积分与微分几何传统的流体力学依赖于矢量微积分，其运算依赖于大量的公式和技巧，相比之下，张量语言作为一种高级数学工具，可以极大地...。

理解纳维尔，斯托克斯方程纳维尔，斯托克斯方程是一组非线性的微分方程，描述了流体的运动，它由法国工程师克劳德，路易·纳维和爱尔兰数学家乔治·加布里埃尔·斯托克斯于19世纪提出，纳维尔，斯托克斯方程与牛顿运动定律的关系纳维尔，斯托克斯方程可以看作是牛顿第二运动定律在流体中的应用，牛顿第二运动定律指出，物体的加速度与其质量和作用于物体的合力...。

引言纳维尔，斯托克斯方程是流体力学中描述流体运动的基本方程，它以数学的形式表达了流体在受力作用下的运动规律，本文将探讨纳维尔，斯托克斯方程的理解方式，及其与牛顿运动定律之间的关联，张量语言在流体力学中的应用张量语言是一种数学语言，可以用来简洁地描述具有多重分量的物理量，在流体力学中，利用张量语言可以大幅简化矢量计算，减少技术细节的干扰...。

纳维尔，斯托克斯方程是流体力学中的一个方程组，描述了流体的运动，该方程组可以通过张量语言来简化，这是一个强大的数学工具，可以在矢量微积分中使用，纳维尔，斯托克斯方程纳维尔，斯托克斯方程可以表示为，$$\rho\frac，\partial\mathbf，v，\partialt，\rho，\mathbf，v，\cdot\nabla，...。

引言纳维尔，斯托克斯方程是一组偏微分方程，描述了不可压缩、粘性流体的运动，它是流体力学的基础，在工程、气象学和其他领域有广泛的应用，纳维尔，斯托克斯方程以其复杂性和难以求解而闻名，本篇文章将深入解析纳维尔，斯托克斯方程，探索它与牛顿运动定律之间的联系，以及如何利用张量语言简化流体力学中的矢量计算，张量语言在流体力学中的应用张量语言是一...。

纳维尔，斯托克斯方程是一组偏微分方程，描述了粘性流体的运动，它们是流体力学中的基本方程，广泛用于建模液体和气体的流动，例如水流、空气流和血液流动，与牛顿运动定律的关联纳维尔，斯托克斯方程是牛顿运动定律在流体中的应用，牛顿第二运动定律指出，作用在物体上的合力等于其质量乘以加速度，纳维尔，斯托克斯方程提供了流体微元的合力的具体表达式，从而...。